Difference between revisions of "Lattice disregistry method"

Latest revision as of 11:05, 20 January 2022

Backgroud

The elastic strain energy at the interface depends on the relative difference of atomic spacing at the two-phase interface, which is called disregistry. The size of interface disregistry reflects the stability of two-phase interface bonding and interface stress state. As the basic interface structure parameter, the current mainstream calculation method -Bramfitt formula[1] is applicable to all crystal structures, but it is necessary to judge the base phase and nucleation phase[2-3]. Moreover, the calculation process is complex and the application scenario is limited to the solidification process. The value of interface disregistry may not be unique, and there are many calculation steps. It is difficult to use a quick way to calculate the interface mismatch for complex crystals.

In this calculation method, the phase information is obtained by introducing two phase3D structures, and the interface disregistry between the two phases is calculated through the construction of supercell, crystal plane index, atomic dense arrangement plane and two-dimensional lattice. The traditional calculation method for judging the base phase and nucleation phase is avoided, so that the user can obtain the interface disregistry degree between the two phase interfaces only by importing the structuresof the phase, and the automatic interface disregistry degree calculation is realized. The calculation of interface disregistry is simplified and the previous limitations are well solved.

Method

In this method, the relevant information is obtained by introducing the structures of the phase, and then the supercell of the phase is constructed by using the relevant knowledge of strapdown inertial navigation and projection[4], so as to obtain the atomic coordinate information and relevant supercell model after cell expansion. The conversion formula is shown in Figure 2. In the above figure, PUV (U, v = x, y, z) represents the projection size of the unit vector on V to the unit vector on u, where B is the rectangular coordinate system and a is other coordinate systems. Through the transformation formula, the atomic coordinate information, the spatial relationship between atoms and the related supercell model are obtained.

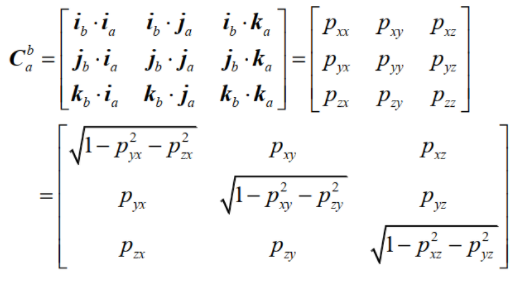
In this calculation method, the atomic coordinate information of the supercell will be obtained. Through the way that every three atoms in the original cell form a plane and the combination of arrangement and combination, the atomic dense plane with the highest atomic density in the supercell of two phases will be calculated cyclically, so as to obtain the indices of crystallographic plane and the distribution of two-dimensional lattice, so as to lay a foundation for the calculation of interface disregistry.

As the basic interface structure parameter, the current mainstream disregistry calculation method - Bramfitt formula is applicable to all crystal structures, but it is necessary to judge the base phase and nucleation phase. The calculation process is complex and the application scenario is limited to the solidification process. The value of interface disregistry may not be unique. There is no one-to-one correspondence between interface structure and interface disregistry value, which is not conducive to the construction of interface database and brings challenges to the research and development of data-driven related materials. Therefore, it is a technical problem to accurately calculate the material interface disregistry and obtain the interface relationship.

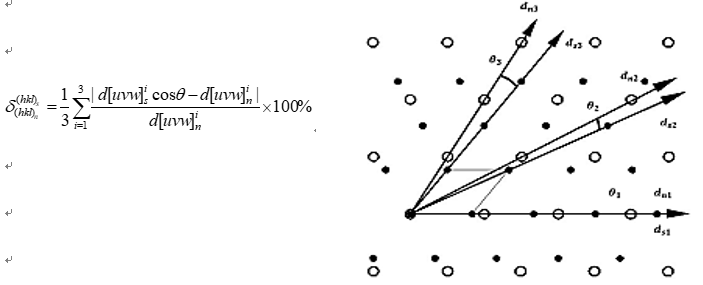
Fig. 3 is the Bramfitt formula and its schematic diagram, [d[uvw]]si 、[d[uvw]]ni represents the atomic spacing of the base phase down from the [uvw] crystal and the atomic spacing of the nucleation phase down from the [uvw] crystal, θ Is the angle between two crystal directions. The mismatch calculation method is further improved based on Bramfitt formula. First calculate the mismatch degree of the diagonal edge, judge the order of both sides according to the atomic spacing of the diagonal edge, and then calculate the average value. Figure 3 is a schematic diagram, d_s^i，d_n^i represents the downward atomic spacing of different phases and crystals, θ Is the angle between two crystal directions.

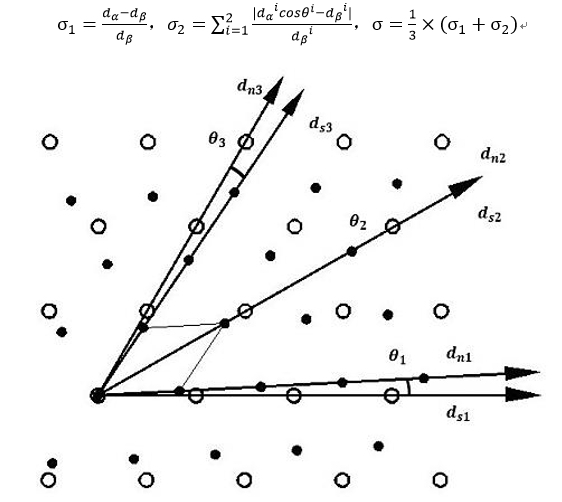
As shown in Figure 4, this method uses Bramfitt's calculation formula on two-dimensional disregistry for reference and improves the formula, so as to avoid judging the base phase and nucleation phase. The calculation process is also convenient and the value is unique. Any interface structure is one-to-one corresponding to the interface disregistry value, which solves the previous limitations.

In this way, through the calculation workflow of interface disregistry, the user can obtain the indices of crystallographic plane, two-dimensional lattice distribution and interface disregistry between the two phasetwo-phase interfaces only by importing the Poscar 3D structures of the phase, and realize the automatic calculation of interface mismatch degree.

References

[1] Bruce L. Bramfitt. The effect of arbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. 1970, 1(10):2958-2958

[2] 潘宁,宋波,翟启杰,文彬.钢液非均质形核触媒效用的点阵错配度理论[J].北京科技大学学报,2010,32(02):179-182+190.

[3] Wang, L.,Yang, L.,Zhang, D., et al., The Role of Lattice Misfit on Heterogeneous Nucleation of Pure Aluminum. Metallurgical and Materials Transactions A 2016, 47 (10), 5012-5022

[4]严恭敏，翁浚.《捷联惯导算法与组合导航原理讲义》.西北工业大学